Math analysis of IRR of typical MBS cashflows.

I came across a problem: calculation of the IRR (internal rate of return) of the cashflows in a context of mortgage-backed securities (MBS). It's a very common problem, and even MS Excel has related functions NPV and IRR. I thought that there should be many algorithms and libraries, which would compute IRR for any given cashflows.

Well, it's true there are many implementations avalable such as the one in the book Financial Numerical Recipes. However, the problem is that we have to compute literally hundreds of thousands IRRs, and I couldn't find an algorithm, which would always find IRR. I think that most of them, like Excel, use some variation of Newton-Raphson algorithm. For example, in our case sometimes up to 1% of IRRs were not found or "wrong" IRRs were returned.

By "wrong" IRR, I mean IRR less than -1, such as -1.6, i.e. -160% monthly interest rate. The problem is that there's another IRR for the same cashflow, which is a "good" one, it was 0.25, i.e. 25% monthly. Such cases were labeled wrongly "miltiple IRR" cases. However, we'll see later on that the problem is not the multiplicity of IRRs, but the fact that our routines find IRRs on the left side of IRR = -1. These IRRs produce amortization schedules which are unacceptable for certain reasons.

I came up with an algorithm, which almost always finds good IRR, but I'll write about it later. Here, I'm going to share with you my little math analysis of typical MBS cashflows.

The typical MBS cashflow is the one with initial payment (outflow) and subsequent cash inflows. So, if Cm is the cashflow amount of month 'm', then C1 < 0, and all other Cm > 0. For example, C1 = -100$ - initial payment, then C2 = 10$ and C3 = 110 cash inflows.

Net present value (NPV) of the cashflow is a sum of terms: Cm/(1+r)^m , where m - is month number, Cm - cashflow amount, r - interest rate. So, in our case it's C1/(1+r)+C2/(1+r)^2+C3/(1+r)^3. IRR is defines as interest rate r, such that NPV(r)=0. In our example it's 0.1, or 10% monthly, see:

Month	Cashflow	IRR	NPV(IRR)
1	-100	0.1	-0.000000000000028
2	10
3	110

A bfrief analysis of the NPV function, given the assumptions of "typical MBS cashflows", brings the following results:

1. As it's shows on figure 1, there's at least one real IRR, which is greater than -1, because NPV(-1) is positive and NPV(infinity) is negative on the right side of -1 rate.
   
2. If Cn*(-1)^n > 0, where n - last month with non-zero cashflow amount, then NPV(-1) is positive and NPV(infinity) is positive on the left side of -1 rate. This means that we can't say if there's real IRR on left side. See figure 2.
   
   
3. If Cn*(-1)^n < 0, where n - last month with non-zero cashflow amount, then NPV(-1) is negative and NPV(infinity) is positive on the left side of -1 rate. This means that there's at least one IRR on left side. See figure 3.
   

Since we have Cn positive, then cases 2 and 3 degenerate to a condition (-1)^n.

You can look at my notes on how I came to above conclusions in the 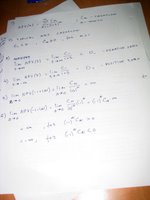next picture. Basic idea is too look at behaviour of NPV near rate values of -1 and negative and positive infinities. Near rate equal to -1, the latest cashflow amounts (which is positive) is most significant, because 1/(1+r)^n is the most significant term.

On the other hand, near infinities the most significant term is C1 (initial payment), because 1/(1+r) is the most significant.

Conclusion for "typical MBS cashflows":

1. there's always real IRR between -1 and positive infinity.
   
2. if the month number of the last non-zero cashflow amount is odd, then there's at least one real IRR between -1 and negative infinity.
   
3. quite often there are more than one real IRRs.
   

Enjoy!